Presenting Elliot’s Hydrogen Fusion Simulator, V1.0.0
It is fairly well accepted that the future of energy will be nuclear. The concept of a Dyson Sphere was first developed by Olaf Stapledon in his science fiction novel Star Maker (1937). The idea was further developed by the physicist Freeman Dyson in his 1960 paper “Search for Artificial Stellar Sources of Infrared Radiation“. Dyson speculated that such structures would be the logical consequence of the escalating energy needs of a technological civilization and would be a necessity for its long-term survival; the light signatures of such structures surrounding stars could be an indicator of extraterrestrial intelligence.

Other hypothetical mega structures include ring worlds, such as the one seen in in the film Elysium, and Alderson disks both of which would harness the energies of the sun.
While this is a possible path for an advanced civilization to take, it would undoubtedly have a negative effect on the on the home world, especially on a water world such as our own. Or, perhaps it could allow for the civilization to control the home world’s atmosphere and radiation levels at a more granular level, through containing and perhaps even sustaining the fusion processes of the Sun with powerfully reflective and absorbent magnetic fields.
Fusion is a gateway to the Stars
Harnessing the power of fusion is an obvious next step for humanity. As we progress scientifically, capturing the massive amounts of energy from the sun are becoming more and more of a priority. The concept of a Dyson sphere, or solar containment structure is all too wonderful; to be able to harness and manipulate the most powerful energy source we can currently explain. Black hole radiation is still poorly understood, as we cannot explain how a body that traps all light and energy could also release massive radiation, so we will set aside this possibility for a bit.
Understanding the Solar Environment
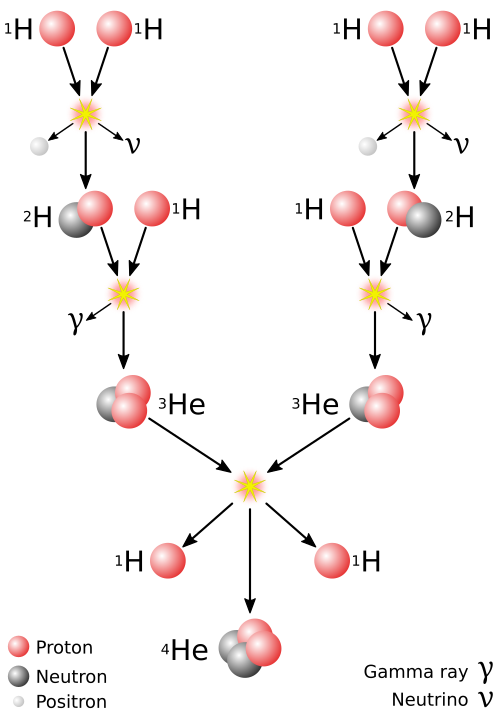
The first task for achieving progress towards any of these technological advancements we must first understand the nature of the Sun. The Sun creates energy through the fusion process known as the Proton-Proton chain where alpha particles are released and hydrogen fuses to become Deuterium, Tritium, and then Helium, which takes a tremendous amount of time. Since the conversion of hydrogen to helium is slow, the complete conversion of the hydrogen initially in the core of the Sun is calculated to take more than ten billion years.[5]
Every second the Sun releases about 3.8 x 10²⁶ joules. That means a second of energy from the Sun could power all of the electricity on planet Earth for 180 years or so. The Sun emits approximately 560 trillion times more energy in a year than Earth consumes. So obviously the Dyson sphere would be very useful for any type of advanced civilization.
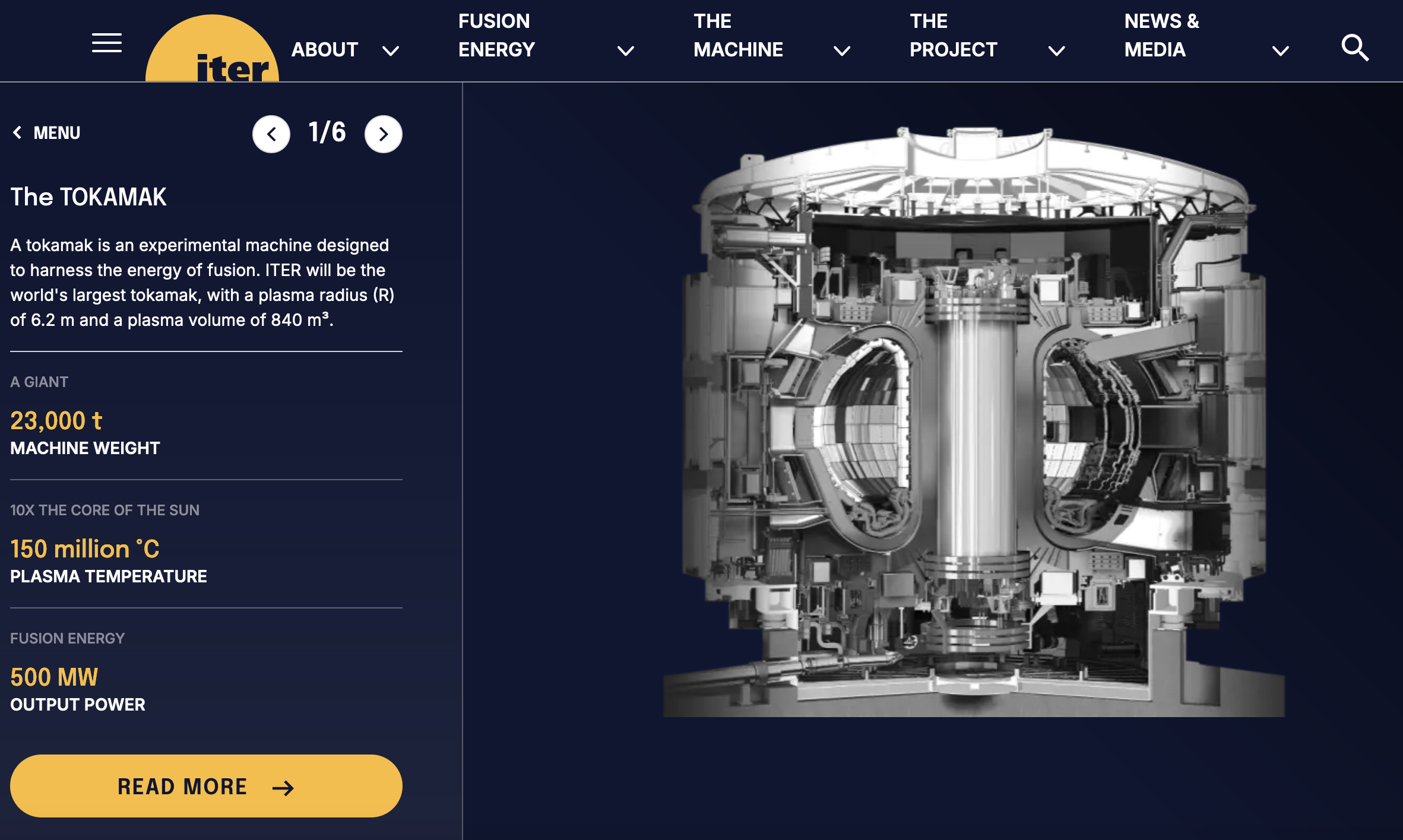
However, it maybe be more practical; at least here on Earth, to create an energy source that is similar to the sun. The break-even point of such a reaction would be tremendous, as the plasma fusion process happens at millions of degrees. ITER’s Tokamak design is planned to achieve around 150 million degrees and will hopefully prove out that the concept is viable. There are other fusion reactor design that could also be possible, and more effective at energy production, such as the stellarator design, or spheromaks, but currently the Tokamak design is expected to reveal the technical limitations and bottlenecks for the fusion process.
ITER will demonstrate this through the magnetic confinement, inertial confinement, and advanced fuels necessary to achieve fusion. The magnetic confinement is very difficult and requires advanced materials.
Simulating Fusion Processes
In order to simulate fusion, the properties and behaviors of Hydrogen, the fuel of the sun, must be explored. Patterning the release of tritium, deuterium, ionized hydrogen particles and electrons will be a key to understand how to create a plasma wind that can create large amounts of energy through the fusion process.
Using Numpy, Numba and Pytorch, in a pygame environment, I have create a machine learning model for understand the particle behaviors in a fusion reactor. The simulation utilizes the concept of ideal confinement, that is to say that the magnetic repulsion barrier for the particles is 100% effective. Obviously in any real environment, especially those on Earth, this would be a far less efficient and would require containment physics, which are not present in this simulation (for obvious reasons once you see the size of the code base).
Imported libraries for the Sim
import numpy as np
import pygame
from numba import njit, prange
import sys
import torch
import torch.nn as nn
import torch.optim as optim
from scipy.interpolate import interp1dConstants for the Hydrogen Plasma Simulator
E_CHARGE = 1.60217662e-19 # Elementary charge (C)
E_MASS = 9.10938356e-31 # Electron mass (kg)
D_MASS = 3.343583719e-27 # Deuteron mass (kg)
T_MASS = 5.0073567446e-27 # Triton mass (kg)
HE_MASS = 6.644657230e-27 # Alpha particle mass (kg)
NEUTRON_MASS = 1.674927471e-27 # Neutron mass (kg)
EPS_0 = 8.854187817e-12 # Vacuum permittivity (F/m)
MU_0 = 4e-7 * np.pi # Vacuum permeability (H/m)
K_B = 1.380649e-23 # Boltzmann constant (J/K)
EV_TO_J = 1.602176634e-19 # Electronvolt to joules conversionVariables to be Adjusted depending on your Computer
# ------------------------
# Simulation Parameters
# ------------------------
INCLUDE_ELECTRONS = True
# Particle counts
NUM_DEUTERIUM = 50
NUM_TRITIUM = 50
NUM_ELECTRONS = 100 if INCLUDE_ELECTRONS else 0
NUM_PARTICLES = NUM_DEUTERIUM + NUM_TRITIUM + NUM_ELECTRONS
# Domain and grid
DOMAIN_SIZE = 1e-4 # Domain size (m)
GRID_SIZE = 100 # Number of grid cells in each dimension
DX = DOMAIN_SIZE / GRID_SIZE # Grid spacing (m)
# Time parameters
DT = 1e-10 # Time step (s)
NUM_STEPS = 5000 # Number of simulation steps
# Plasma parameters
TEMPERATURE = 1e6 # Initial plasma temperature (K)
# Magnetic field
B0 = 5.0 # Magnetic field strength (T)
# Fusion parameters
FUSION_SCALING_FACTOR = 1e30 # Increased scaling factor for fusion probability
# Collision parameters
R_COLL = DOMAIN_SIZE / GRID_SIZE * 2.0 # Collision radius (m)
R_MAG = DOMAIN_SIZE / GRID_SIZE * 1.0 # Magnetic interaction radius (m)
# Visualization parameters
SCREEN_SIZE = 800 # Screen size in pixels
PARTICLE_SIZE = 4 # Particle radius in pixels
FPS = 60 # Frames per second
# Runtime Warning Fix Parameters
MIN_DISTANCE = 1e-12 # Minimum distance to prevent division by zero
MAX_FORCE = 1e5 # Maximum allowed force magnitudeKey Features of the Simulation
There are many functions in this simulation, I was really pushing my M1 to its limits. The particle count could be scaled up as well as the fusion probabilities if I had say a nice and powerful GPU supported super-computer to test on.
- Particle Behavior simulation within a magnetically confined environment
- Particle Trails for understand the behavior of higher energy particles and to display velocities
- Machine Learning for fusion event probabilities an associated energy conversions
- Total Environment Charge calculations
- Particle Velocity and Mass Computations
- Particle Additions with clicks/keyboard Strokes
- d key / Left Mouse click – add deuterium particle
- t key / middle mouse click – add tritium particle
- e key / right mouse click – add electron particle
- Field and Convergence calculations
- Spatial Particle Collision calculations
- Alpha particle behaviors
- Neutron particle behaviors
- Fusion Event Counter
Boris Push Function –
a leapfrog scheme, where the particle is moved, then half of the energy changed is applied. After this, the momentum is rotated by the B field, and the rest of the energy change applied.
def boris_push(positions, velocities, charges, masses, Ex, Ey, Bz, dt, grid_size, domain_size):
num_particles = positions.shape[0]
for i in prange(num_particles):
# Get particle's grid indices
x_idx = int(positions[i, 0] / domain_size * grid_size)
y_idx = int(positions[i, 1] / domain_size * grid_size)
# Clamp indices to grid boundaries
if x_idx >= grid_size:
x_idx = grid_size - 1
elif x_idx < 0:
x_idx = 0
if y_idx >= grid_size:
y_idx = grid_size - 1
elif y_idx < 0:
y_idx = 0
# Get electric and magnetic fields at particle's position
E_particle = np.array([Ex[x_idx, y_idx], Ey[x_idx, y_idx]])
B_particle_z = Bz[x_idx, y_idx] # Magnetic field in z-direction
# Charge-to-mass ratio
qm = charges[i] / masses[i]
# Half acceleration due to electric field
velocities[i] += qm * E_particle * (dt / 2.0)
# Rotation due to magnetic field (B only in z)
t = qm * B_particle_z * (dt / 2.0)
s = 2.0 * t / (1.0 + t * t)
v_minus = velocities[i]
# Cross product in 2D (magnetic field only in z, velocities in x and y)
v_prime_x = v_minus[0] + v_minus[1] * t
v_prime_y = v_minus[1] - v_minus[0] * t
v_prime = np.array([v_prime_x, v_prime_y])
velocities[i] = v_minus + s * v_prime
# Half acceleration due to electric field
velocities[i] += qm * E_particle * (dt / 2.0)
# Update positions
positions[i] += velocities[i] * dt
# Reflective boundary conditions with clamping
for dim in range(2): # x and y
if positions[i, dim] < 0:
positions[i, dim] = -positions[i, dim]
velocities[i, dim] = -velocities[i, dim]
elif positions[i, dim] > domain_size:
positions[i, dim] = 2 * domain_size - positions[i, dim]
velocities[i, dim] = -velocities[i, dim]
# **Explicit Clamping (Additional Safeguard)**
positions[i, 0] = min(max(positions[i, 0], 0.0), domain_size)
positions[i, 1] = min(max(positions[i, 1], 0.0), domain_size)
return positions, velocitiesParticle Pairing through Magnetic Forces
def compute_pairwise_magnetic_forces(positions, velocities, charges, masses, R_mag, mu_0, dt):
"""
Compute pairwise magnetic forces between charged particles.
Simplified 2D magnetic force calculation.
Returns:
F_mag: Array of shape (num_particles, 2) representing magnetic forces.
"""
num_particles = positions.shape[0]
F_mag = np.zeros((num_particles, 2), dtype=np.float64)
for i in prange(num_particles):
for j in range(i + 1, num_particles):
r_vec = positions[j] - positions[i]
distance = np.linalg.norm(r_vec)
if distance < R_mag and distance > MIN_DISTANCE:
# Simplified magnetic force calculation
v1 = velocities[i]
v2 = velocities[j]
v_rel = v1 - v2
r_hat = r_vec / distance
# Relative velocity perpendicular component
v_rel_perp = v_rel - np.dot(v_rel, r_hat) * r_hat
# Force magnitude
F = (mu_0 / (4 * np.pi)) * (charges[i] * charges[j] * np.linalg.norm(v_rel_perp)) / (distance ** 2)
# Clamp force to prevent overflow
if F > MAX_FORCE:
F = MAX_FORCE
elif F < -MAX_FORCE:
F = -MAX_FORCE
# Direction: perpendicular to r_vec
perp_dir = np.array([-r_hat[1], r_hat[0]])
F_vector = F * perp_dir * dt
F_mag[i] += F_vector
F_mag[j] -= F_vector # Newton's third law
return F_mag
def identify_significant_pairs(F_mag, positions, velocities, charges, species, threshold=1e-25):
"""
Identify particle pairs experiencing significant magnetic forces.
Args:
F_mag (np.ndarray): Array of shape (num_particles, 2) representing magnetic forces.
positions (np.ndarray): Array of shape (num_particles, 2) representing positions.
velocities (np.ndarray): Array of shape (num_particles, 2) representing velocities.
charges (np.ndarray): Array of shape (num_particles,) representing charges.
species (np.ndarray): Array of shape (num_particles,) representing species.
threshold (float): Threshold for force magnitude to consider significant.
Returns:
significant_pairs (list of tuples): List of particle index pairs with significant forces.
"""
significant_pairs = []
num_particles = positions.shape[0]
for i in range(num_particles):
for j in range(i + 1, num_particles):
# Compute force magnitude between particles i and j
r_vec = positions[j] - positions[i]
distance = np.linalg.norm(r_vec)
if distance < R_MAG and distance > MIN_DISTANCE:
# Simplified magnetic force calculation (same as in Numba function)
v_rel = velocities[i] - velocities[j]
if distance > 0:
r_hat = r_vec / distance
else:
r_hat = np.array([0.0, 0.0])
v_rel_perp = v_rel - np.dot(v_rel, r_hat) * r_hat
F = (MU_0 / (4 * np.pi)) * (charges[i] * charges[j] * np.linalg.norm(v_rel_perp)) / (distance ** 2)
if F > threshold:
significant_pairs.append((i, j))
return significant_pairsParticle Fusion Simulation Parameters
def attempt_fusion_spatial(positions, velocities, charges, masses, species, dt, grid_size, domain_size):
fusion_events = []
# Calculate cell indices for all particles
cell_indices_x = (positions[:, 0] / domain_size * grid_size).astype(np.int32)
cell_indices_y = (positions[:, 1] / domain_size * grid_size).astype(np.int32)
# Clamp indices to grid boundaries
cell_indices_x = np.clip(cell_indices_x, 0, grid_size - 1)
cell_indices_y = np.clip(cell_indices_y, 0, grid_size - 1)
# Spatial grid for efficient collision detection
grid = {}
for idx in range(len(positions)):
key = (cell_indices_x[idx], cell_indices_y[idx])
if key in grid:
grid[key].append(idx)
else:
grid[key] = [idx]
# Iterate through grid cells and their neighbors for potential fusion
for key, particle_indices in grid.items():
neighbors = []
x, y = key
for dx_cell in [-1, 0, 1]:
for dy_cell in [-1, 0, 1]:
neighbor_key = (x + dx_cell, y + dy_cell)
if neighbor_key in grid:
neighbors.extend(grid[neighbor_key])
for i in particle_indices:
for j in neighbors:
if j <= i:
continue # Avoid duplicate checks
# Check if one is deuterium and the other is tritium
if ((species[i] == 0 and species[j] == 1) or
(species[i] == 1 and species[j] == 0)):
# Calculate distance
distance = np.linalg.norm(positions[i] - positions[j])
if distance > R_COLL:
continue # Beyond collision radius
# Calculate relative kinetic energy (J)
relative_velocity = compute_relative_velocity(velocities[i], velocities[j])
kinetic_energy_J = 0.5 * masses[i] * relative_velocity**2 # Approximation
# Get fusion cross-section (m^2)
sigma = get_fusion_cross_section(kinetic_energy_J)
# Calculate fusion probability
P_fusion = sigma * relative_velocity * dt
P_fusion *= FUSION_SCALING_FACTOR # Artificial scaling
# Clamp probability to [0,1]
P_fusion = min(P_fusion, 1.0)
# Determine if fusion occurs
if np.random.rand() < P_fusion:
fusion_events.append((i, j))
print(f"Fusion Events This Step: {len(fusion_events)}")
return fusion_events
def process_fusion_events(fusion_events, positions, velocities, charges, masses, species, particle_trails):
if not fusion_events:
return positions, velocities, charges, masses, species, particle_trails, 0
fusion_count = 0
removed_indices = set()
new_positions = []
new_velocities = []
new_charges = []
new_masses = []
new_species = []
new_trails = []
for (i, j) in fusion_events:
if i in removed_indices or j in removed_indices:
continue # Skip if already processed
# Mark reactants for removal
removed_indices.add(i)
removed_indices.add(j)
# Calculate the midpoint position for fusion products
mid_pos = (positions[i] + positions[j]) / 2.0
# Calculate total momentum before fusion
total_momentum = masses[i] * velocities[i] + masses[j] * velocities[j]
# Energy distribution (simplified)
energy_alpha = 8.8e6 * EV_TO_J # Energy to alpha particle
energy_neutron = 8.8e6 * EV_TO_J # Energy to neutron
# Velocity calculations based on kinetic energy
v_alpha = np.sqrt(2 * energy_alpha / HE_MASS)
v_neutron = np.sqrt(2 * energy_neutron / NEUTRON_MASS)
# Assign random direction for alpha particle
theta = np.random.uniform(0, 2 * np.pi)
alpha_velocity = v_alpha * np.array([np.cos(theta), np.sin(theta)])
# Neutron velocity ensuring momentum conservation
neutron_velocity = (total_momentum - HE_MASS * alpha_velocity) / NEUTRON_MASS
# Ensure mid_pos is within domain
mid_pos = np.clip(mid_pos, 0.0, DOMAIN_SIZE)
# Append new fusion products
# Alpha Particle: Cyan (0,255,255)
new_positions.append(mid_pos)
new_velocities.append(alpha_velocity)
new_charges.append(2 * E_CHARGE) # Alpha particle charge
new_masses.append(HE_MASS)
new_species.append(3) # Alpha Particle
new_trails.append([]) # Initialize trail for new particle
# Neutron: Magenta (255,0,255)
new_positions.append(mid_pos)
new_velocities.append(neutron_velocity)
new_charges.append(0.0) # Neutron charge
new_masses.append(NEUTRON_MASS)
new_species.append(4) # Neutron
new_trails.append([]) # Initialize trail for new particle
fusion_count += 1
# Create a boolean mask to keep particles not in removed_indices
if removed_indices:
mask = np.ones(len(positions), dtype=bool)
mask[list(removed_indices)] = False
# Apply mask to all relevant arrays
positions = positions[mask]
velocities = velocities[mask]
charges = charges[mask]
masses = masses[mask]
species = species[mask]
# Update particle_trails by removing trails of fused particles
particle_trails = [trail for idx, trail in enumerate(particle_trails) if mask[idx]]
# Add new fusion products to arrays
if new_positions:
# Convert lists to NumPy arrays
new_positions = np.array(new_positions)
new_velocities = np.array(new_velocities)
new_charges = np.array(new_charges)
new_masses = np.array(new_masses)
new_species = np.array(new_species)
# Append to existing arrays
positions = np.vstack([positions, new_positions])
velocities = np.vstack([velocities, new_velocities])
charges = np.hstack([charges, new_charges])
masses = np.hstack([masses, new_masses])
species = np.hstack([species, new_species])
# Append new trails
particle_trails.extend(new_trails)
return positions, velocities, charges, masses, species, particle_trails, fusion_countMain Particle Fusion Simulation Loop
# Main Simulation Loop
# ------------------------
running_simulation = True
step = 0
fusion_count_total = 0 # To keep track of total fusion events
# UI Variables
current_particle_type = 'deuterium' # Default particle type
# End State Variables
MAX_FUSION_EVENTS = 100
neutrality_steps_required = 100
neutrality_counter = 0
previous_energy = None # To be initialized after first energy computation
while running_simulation and step < NUM_STEPS:
# Event handling for Pygame
for event in pygame.event.get():
if event.type == pygame.QUIT:
running_simulation = False
break
elif event.type == pygame.KEYDOWN:
if event.key == pygame.K_q:
running_simulation = False
print("Simulation terminated by user.")
break
elif event.key == pygame.K_d:
current_particle_type = 'deuterium'
print("Selected particle type: Deuterium")
elif event.key == pygame.K_t:
current_particle_type = 'tritium'
print("Selected particle type: Tritium")
elif event.key == pygame.K_e:
current_particle_type = 'electron'
print("Selected particle type: Electron")
elif event.type == pygame.MOUSEBUTTONDOWN:
mouse_pos = pygame.mouse.get_pos()
if event.button == 1: # Left-click
positions, velocities, charges, masses, species, particle_trails = add_particle(
mouse_pos, 'deuterium', positions, velocities, charges, masses, species, particle_trails
)
print(f"Added Deuterium at {mouse_pos}")
elif event.button == 3: # Right-click
positions, velocities, charges, masses, species, particle_trails = add_particle(
mouse_pos, 'tritium', positions, velocities, charges, masses, species, particle_trails
)
print(f"Added Tritium at {mouse_pos}")
elif event.button == 2: # Middle-click
positions, velocities, charges, masses, species, particle_trails = add_particle(
mouse_pos, 'electron', positions, velocities, charges, masses, species, particle_trails
)
print(f"Added Electron at {mouse_pos}")
# Deposit charge
rho = deposit_charge(positions, charges, GRID_SIZE, DOMAIN_SIZE)
# Calculate potential phi with convergence
phi = calculate_phi(rho, DX, EPS_0)
# Calculate electric fields Ex and Ey outside Numba
Ex_padded, Ey_padded = calculate_E_fields(phi, DX)
# Push particles
positions, velocities = boris_push(positions, velocities, charges, masses, Ex_padded, Ey_padded, Bz, DT, GRID_SIZE, DOMAIN_SIZE)
# Compute and apply pairwise magnetic forces
F_mag = compute_pairwise_magnetic_forces(positions, velocities, charges, masses, R_mag=R_MAG, mu_0=MU_0, dt=DT)
velocities += F_mag # Update velocities based on magnetic forces
# Check for invalid values in positions and velocities
valid_mask = validate_particles(charges, velocities)
if not np.all(valid_mask):
num_invalid = np.sum(~valid_mask)
print(f"Step {step}: Invalid Particles Detected = {num_invalid}. Removing them.")
positions = positions[valid_mask]
velocities = velocities[valid_mask]
charges = charges[valid_mask]
masses = masses[valid_mask]
species = species[valid_mask]
# Remove trails for invalid particles
particle_trails = [trail for idx, trail in enumerate(particle_trails) if valid_mask[idx]]
# Identify significant_pairs after ensuring all positions are valid
significant_pairs = identify_significant_pairs(F_mag, positions, velocities, charges, species, threshold=1e-25)
# Attempt fusion with spatial collision detection
fusion_events = attempt_fusion_spatial(positions, velocities, charges, masses, species, DT, GRID_SIZE, DOMAIN_SIZE)
# Process fusion events
if fusion_events:
positions, velocities, charges, masses, species, particle_trails, fusion_count = process_fusion_events(
fusion_events, positions, velocities, charges, masses, species, particle_trails
)
fusion_count_total += fusion_count
# Collect data for machine learning (optional)
for (i, j) in fusion_events:
# Ensure indices are still valid after fusion processing
if i < len(positions) and j < len(positions):
# Features: [x_i, y_i, vx_i, vy_i, x_j, y_j, vx_j, vy_j]
feature = np.concatenate([positions[i], velocities[i], positions[j], velocities[j]])
features.append(feature)
labels.append(1) # Fusion occurred
# Update particle trails
for i in range(len(positions)):
if len(particle_trails[i]) >= trail_length:
particle_trails[i].pop(0) # Remove the oldest position
trail_pos = (
int(positions[i, 0] / DOMAIN_SIZE * SCREEN_SIZE),
int(positions[i, 1] / DOMAIN_SIZE * SCREEN_SIZE)
)
particle_trails[i].append(trail_pos)
# Compute total charge
total_charge = compute_total_charge(rho)
# Compute total energy and check for equilibrium
current_energy = compute_total_energy(rho, phi, velocities, masses, Bz)
if previous_energy is not None:
energy_change = abs(current_energy - previous_energy)
if energy_change < 1e-20:
print("Energy equilibrium reached. Stopping simulation.")
running_simulation = False
previous_energy = current_energy
# Check charge neutrality and monitor velocities every 100 steps
if step % 100 == 0:
if abs(total_charge) < 1e-12:
neutrality_counter += 1
if neutrality_counter >= neutrality_steps_required:
print("Charge neutrality achieved and stable. Stopping simulation.")
running_simulation = False
else:
neutrality_counter = 0
# Optionally enforce charge neutrality
charges = enforce_charge_neutrality(charges)
avg_velocity = np.mean(np.linalg.norm(velocities, axis=1))
max_velocity = monitor_velocities(velocities)
print(f"Step {step}: Avg Velocity = {avg_velocity:.2e} m/s, Max Velocity = {max_velocity:.2e} m/s, Total Charge = {total_charge:.2e} C")
# Visualization
screen.fill((0, 0, 0)) # Clear screen with black
# Draw boundary walls
boundary_color = (255, 255, 255) # White
boundary_thickness = 5
pygame.draw.rect(screen, boundary_color, pygame.Rect(0, 0, SCREEN_SIZE, SCREEN_SIZE), boundary_thickness)
# Optional: Draw magnetic force lines
for (i, j) in significant_pairs:
x1 = int(positions[i, 0] / DOMAIN_SIZE * SCREEN_SIZE)
y1 = int(positions[i, 1] / DOMAIN_SIZE * SCREEN_SIZE)
x2 = int(positions[j, 0] / DOMAIN_SIZE * SCREEN_SIZE)
y2 = int(positions[j, 1] / DOMAIN_SIZE * SCREEN_SIZE)
pygame.draw.line(screen, (0, 0, 255), (x1, y1), (x2, y2), 1) # Blue lines for magnetic forces
# Draw particles and their trails
for i in range(len(positions)):
x = int(positions[i, 0] / DOMAIN_SIZE * SCREEN_SIZE)
y = int(positions[i, 1] / DOMAIN_SIZE * SCREEN_SIZE)
# Ensure particles are within screen bounds
x = min(max(x, 0), SCREEN_SIZE - 1)
y = min(max(y, 0), SCREEN_SIZE - 1)
# Assign colors based on species
if species[i] == 0:
color = (0, 0, 255) # Deuterium: Blue
elif species[i] == 1:
color = (0, 255, 0) # Tritium: Green
elif species[i] == 2:
color = (255, 255, 255) # Electrons: White
elif species[i] == 3:
color = (0, 255, 255) # Alpha Particle: Cyan (combined color)
elif species[i] == 4:
color = (255, 0, 255) # Neutron: Magenta (combined color)
else:
color = (255, 255, 255) # Undefined species: White
# Draw trails
if len(particle_trails[i]) > 1:
pygame.draw.lines(screen, color, False, particle_trails[i], 1)
# Draw the particle
pygame.draw.circle(screen, color, (x, y), PARTICLE_SIZE)
# Display Fusion Count, Step, Total Charge, and Current Particle Type
font = pygame.font.SysFont(None, 24)
fusion_text = font.render(f'Fusion Events: {fusion_count_total}', True, (255, 255, 255))
step_text = font.render(f'Step: {step}', True, (255, 255, 255))
charge_color = (0, 255, 0) if abs(total_charge) < 1e-12 else (255, 0, 0)
charge_text = font.render(f'Total Charge: {total_charge:.2e} C', True, charge_color)
particle_type_text = font.render(f'Current Particle: {current_particle_type.capitalize()}', True, (255, 255, 255))
screen.blit(fusion_text, (10, 10))
screen.blit(step_text, (10, 30))
screen.blit(charge_text, (10, 50))
screen.blit(particle_type_text, (10, 70))
# Update display
pygame.display.flip()
clock.tick(FPS)
step += 1
# Print total fusion events upon completion
print(f"Total Fusion Events: {fusion_count_total}")
# Quit Pygame
pygame.quit()
sys.exit()Fusion Particle Simulation Code available on GitHub.
Feel free to pull the branch on Github and experiment with the code yourself! Due to the complexity of the simulation environment and the fact that it is coded in Python, I can’t easily host the simulator.
Anaconda is probably necessary to run the code, I developed this in tandem with Chat GPT using Jupyter Notebooks (which are a fantastic way to control version and safely utilize your machine for advanced computational analysis). Peer review and critical analysis is more than welcome.
Please feel free to reach out through any medium to contact me about the simulation. I will be advancing this over time, but for now it is an interesting tool to understand how to optimize fusion environments, and to visualize the interactions between particles and their fusion probabilities, which a highly scaled for the computational environment. Enjoy!