The S2 Star and Sagittarius A (orbital simulation)

Requirements: Python3, Numpy

I always like to learn about new concept and ideas, so this morning I woke up and just started to study frame dragging and relativistic effects on stars. I’ve been spending a lot of time with physics lately and have done a full Sagittarius A calculation, which turned out to be a fun way to practice some AI astrophyics and celestial mechanics and work on turning physics Python code; it has since evolved into a full orbital analysis of the S star cluster near Sagittarius A. I will continue to expand this project over time.

Download my Project on Github

S2 – SagA – Orbit Project

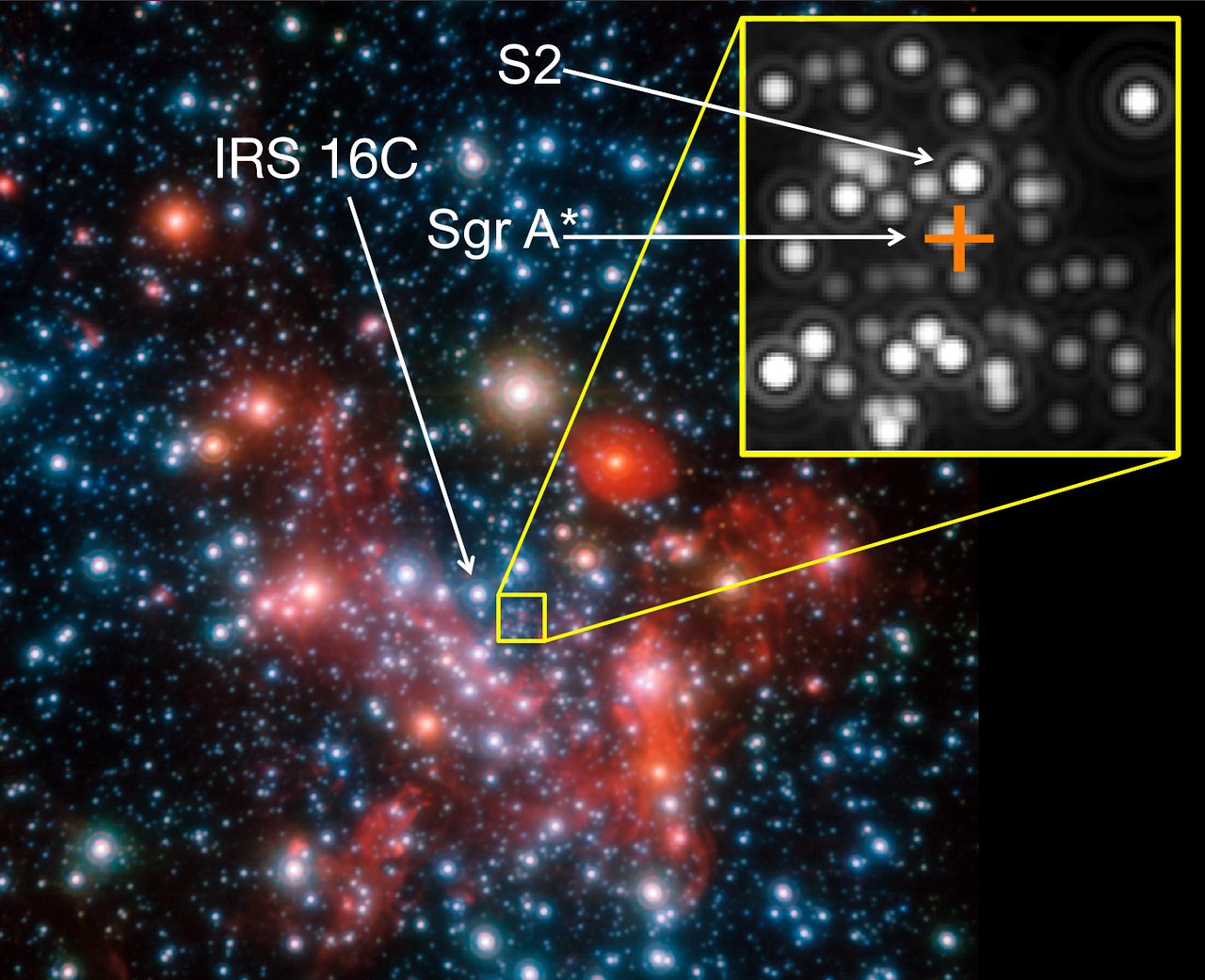
S2 Star – the Laboratory for Relativity

S2 is an incredibly interesting object. It is the subject of hundreds of studies attempting to prove Einstein’s theory of relativity.

S2, also known as S0–2, is a star in the star cluster close to the supermassive black hole Sagittarius A* (Sgr A*), orbiting it with a period of 16.0518 years, a semi-major axis of about 970 au, and a pericenter distance of 17 light hours (18 Tm or 120 au) – an orbit with a period only about 30% longer than that of Jupiter around the Sun, but coming no closer than about four times the distance of Neptune from the Sun – (wikipedia)

The mass when the star first formed is estimated by the European Southern Observatory (ESO) to have been approximately 14 M_☉.^[5] based on its spectral type (B0V ~ B3V).

From the Schwarzchild detection paper: “The robustness of the detection of the SP strongly correlates with the precision of knowing (x₀, y₀, vx₀, and vy₀), as this sets the angle of the orbit at the last apocentre.^[1]” This means that knowing the x and y coordinate changes over time, along with their changes in velocity (vx₀, and vy₀) are the primary necessities for quality imaging and spectroscopy.

Simulating the Orbit of the S2 Star

I have gotten pretty good at programming lately, especially in python, so I decided to create an orbital trajectory analysis for S2. The data is pretty cool, the amount of curvature in the orbit as well as the change in velocity that star experiences is fascinating. You can see that at the peak velocity the star is getting dragged by the tremendous mass of Sagittarius A at a rate of 194km/s. This seems to correspond to the amount of velocity that would be lost to a non-spinning black hole, which obviously Sagittarius A has some angular momentum, though it is supposed to be pretty small relative to other black holes.

The S2 Star Simulation

G = 6.67430e-11 # Gravitational constant
c = 3e8 # Speed of light
M_SagA = 4.154e6 * 1.989e30 # Sagittarius A* mass
J = 0.616 * G * (M_SagA**2) / c # Angular momentum
AU = 1.496e11 # Astronomical Unit

The left/right arrow keys increase and decrease the speed of the simulation and the up/down arrow keys adjust the zoom level of the simulation, that is centered on the black hole. There is a simple Camera Class, and a game loop for the animation that was made with Pygame, a really awesome little 2D game library that I use for all kinds of lightweight animations. For the heavier animations, I generally use shader code and three.js and the WebGL library for creating 3D environments.

The trajectory of S2 is extraordinarily elliptical. The star is certainly increasing and decreasing momentum with lots of delta. This little piece of Python software was made to understand it better. I spent a bit of time on the UI just to make the velocity changes visible and allow the time scale to be adjusted so that I could analyze the trajectory around Sag A, which is the most dynamic part of the simulation and would fail if it wasn’t approximated. In reality, there are so many variables involved in larger calculations like this. The trajectory of the orbit is pretty visible and I enjoy watching the limits of the computer breakdown as the velocities reach impossible speeds due to the time factor being increased. There is a lot of room for expansion here, and I think that actually describing orbital perturbations will be extremely important to truly understanding what the environment around a Super Massive Black Hole is like.

Check out my simulation code:

S2 Simulation Code from Github

Analyzing Sagittarius A, the Mysterious Black Hole at the Center of the Milky Way Galaxy

Elliot’s code for S2’s Orbit and Sagittarius A Spin Analysis Simulation with S2, S62, S4716, S4711, S4716

There are two giant variables missing from the above analysis, mostly having to do with the spin and gravity of Sagittarius A. At the present I am working on a second simulation involving more of the variables from the environment, specifically the spin of Sag A, but also frame dragging effects via the Lense-Thirring effect of frame dragging on Einstein’s curved space-time, of which we have done the initial calculus with S2 via the velocity calculation simulation above. This is a correlate of and interconnected to the time dilation variables (ie. how much time will slow as a body approaches the black hole, or Schwartzchild radius). Undoubtedly, the two must be calculated and integrated individually and then together to understand what the accretion disc environment of Sagittarius A is truly like.

Conclusion

This a good start to beginning a more fully organized and comprehensive analysis of the Sagittarius A environment, especially the S2 star, but also the several other stars of the Sag A environment that are truly fascinating, including:

S2 – 7,000 kilometers per second, this is about 1/60 the speed of light
S62 – 30,000 kilometers per second, 10% of the speed of light
S4711 – 20,000 kilometers per second, which is about 6.7% of the speed of light.
S4714 – 24,000 km/second. 8% of light speed, or 15,000 miles per second
S4716 – 8,000 kilometers per second (5,000 miles per second). This is about 2.6% the speed of light

For reference, the speed of light is largely accepted to be: 300,000 kilometers per second (km/s)